Characterization of near-surface spatial variation of ground structure in Argostoli by ambient vibration (>1Hz)
In addition to already existing 6 months noise recordings on a 21 element array site (interstation distance ranging from 5 to 160 m) in Argostoli site, specific ambient noise measurements are performed by using 65 geophones (3 components) of the high resolution mobile tool recently acquired by the French national mobile pool (Sismob/INSU). These stations will be deployed over a 160 m X 160 m area for a 1 week period. By using noise interferometry, we will test the ability of the above 65 element array to provide fine image of the spatial variation of the near-surface ground structure (down to 20 m depth), compared to classical extensive geophysical experiments (shear-wave seismic tomography, resistivity profiles). Spatial correlation model in terms of coefficient of variation of shear-wave velocity and correlation length will then be estimated and feed the numerical models of WP2 and WP3.

Characterization of spatial variation of ground motion from noise and earthquake data
Wave field composition and coherency functions from earthquake recordings have already been derived at Argostoli site on sediment and rock formations in former projects. The objective of this task is to explore how the seismic noise can help to overcome the lack of instrumental data to provide robust and quantitative indicators on both the amplitude and the phase spatial variability of seismic motion and, hereafter, the coherency functions. Time variation of noise properties and composition (Rayleigh/Love waves) will first be investigated by means of array or polarization analysis. Next, coherency functions (unlagged, lagged and plane-wave) will be derived from the noise recordings including use of specific seismic phases or not, and the time necessary to obtain stability of coherency estimates is evaluated. The coherency estimated from noise will be compared to that determined from the seismic records in order to analyze whether coherency estimates from noise and earthquakes are consistent. We furthermore extend and validate the analytical Uscinski-Sato coherency model to the case where the spatial correlation length is not the same in the three spatial directions and assess its adequateness for Argostoli data. We investigate the possibility to infer the correlation length and COV from ambient noise by means of the parametric coherency function.
We also use a non-parametric method, called multidimensional correlation mapping to represent the local spatial correlation of the ground motion by contour plots of equal correlation with respect to the central station of the array. Contrary to the spatial coherency, this method estimates spatial correlation without presuming homogeneity or isotropy of the phase-aligned local ground motion fields. This allows to assess the variation of correlation levels over a 2D space and also with respect to the direction of the dominant wave direction and frequency of the motions. Finally, the results will be compared to those obtained in the Task 1.1.

Characterization of near-surface spatial variation of ground structure in Grenoble
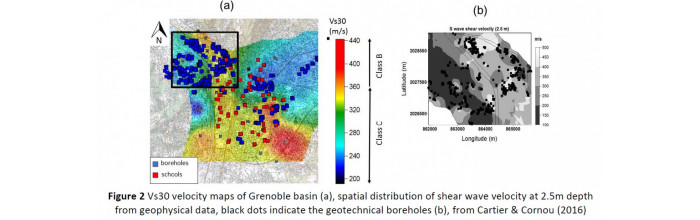
Numerous geophysical experiments over the past years together with analysis of about 1500 geotechnical boreholes have allowed to derive a first “smooth” 3D velocity model (see Figure 2) over the first 30 meters of Grenoble basin. In this task, we will focus on deriving spatial correlation models for the main surficial geological units by making best use of available information and to propose a 3D velocity model that includes both deep sediments mechanical properties and geometry and variable properties of near surface layers that will be modeled as random fields in WP2 and WP3.